| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- maplotlib
- MacOS
- SQL
- 등차수열
- 재귀함수
- 자료구조
- 파이썬
- plt
- 조합
- python
- Slicing
- 리스트
- pandas
- numpy
- 등비수열
- INSERT
- Machine Learning
- 통계학
- pandas filter
- 기계학습
- pandas 메소드
- matplotlib
- barh
- 스터디노트
- Folium
- DataFrame
- tree.fit
- 머신러닝
- 순열
- 문제풀이
Archives
- Today
- Total
코딩하는 타코야끼
[스터디 노트] Week10_2일차 [기본] - 통계학 본문
728x90
반응형
1. 이산형 확률 분포

📍 확률 분포(probability distribution)
- 확률 변수 X가 취할 수 있는 모든 값과 그 값을 나타날 확률을 표현한 함수

📍 이산형 균등 분포(discrete uniform distribution)
- 확률 변수 X가 유한개이고, 모든 확률 변수에 대하여 균일한 확률을 갖는 분포를 이산형 균등 분포라고 함


📍 베르누이 시행(Bernoulli trial)
- 각 시행의 결과가 성공, 실패 두가지 결과만 존재하는 시행을 베르누이 시행이라고 한다.
- 베르누이 시행에서 성공이 ‘1’, 실패가 ‘0’의 값을 갖을 때 확률 변수 X의 분포를 베르누이 분포(Bernoulli distribution)라고 하며, 다음과 같이 정의함


⚡️ 예제)
- 파란공 7개, 빨간공 3개가 들어있는 주머니에서 공 하나를 뽑을 때, 파란공이면 성공 빨란공이라면 실패인 실험을 한다고 가정하자. 이때 베르누이 분포를 정의하면

📍 이항분포(Binomial distribution)
- 연속적인 베르누이 시행을 거처 나타나는 확률 분포이다.
- 서로 독립인 베르누이 시행을 n번 반복해서 실행 했을 때, 성공한 횟수 X의 확률 분포이다.


⚡️ 예제)
- 축구선수의 패널티킥 성공률이 80%일때, 10번의 기회에서 성공횟수와 그 확률을 구하면 아래와 같다.

- 반도체 공장에서 불량이 발생할 확률이 10%라고 하자. 10개의 제품을 생성했을때 불량이 2개 이하일 확률을 구하시오

📍 포아송 분포(Poisson distribution)
- 어느 희귀한 사건이 어떤 일정한 시간대에 특정한 사건이 발생할 확률 분포 임
- 예시) 야구장에서 파울볼을 잡을 횟수, 버스 정류장에서 특정 버스가 5분 이내에 도착한 횟수, 1년간 지구에 1미터 이상의 운석이 떨어지는 수 등
⚡️ 포아송 분포의 조건
- 어떤 단위구간(예, 1일)동안 이를 더 짧은 작은 단위의 구간(예: 1시간)로 나눌 수 있고 이러한 더 짧은 단위구간 중에 어떤 사건이 발생할 확률은 전체 척도 중에서 항상 일정
- 두 개 이상의 사건이 동시에 발생할 확률은 0에 가까움
- 어떤 단위구간의 사건의 발생은 다른 단위구간의 발생으로부터 독립적임
- 특정 구간에서의 사건 발생확률은 그 구간의 크기에 비례함
- 포아송분포 확률 변수의 기댓값과 분산은 모두 λ 임
⚡️ 예제)
야구장에서 경기당 홈런볼을 잡는 관객이 평균 3명 이라고 가정하자
- 오늘 경기에서 2명 이상이 홈런볼을 잡을 확률을 구하시오
- 오늘과 내일 동안 경기에서 홈런볼을 잡지 못할 확률을 구하시오

📍 이항 분포의 포아송 근사
- 확률 변수 X가 X ~ B(n,p)이고, n이 충분히 크고, p가 아주 작을 때, X의 분포는 평균이 . = x인 포아송 분포로 근사 시킬 수 있다.
- 보통 n이 클때, np<5를 만족하게 p가 작으면 근사 정도가 좋다고 함 X ~ Poisson(np)

📍 기하분포(geometric distribution)
- 어떤 실험에서 처음 성공이 발생하기 까지 시도한 횟수 X의 분포, 이때 각 시도는 베르누이 시행을 따른다



⚡️ 예시)
- 축구선수 손흥민의 필드골 성공 확률이 30%일 때, 5번째 슛팅에서 골을 넣을 확률 분포

📍음이항분포(negative binomial distribution)
- 어떤 실험에서 성공확률이 p일 때, r번의 실패가 나올 때 까지 발생한 성공 횟수 X의 확률 분포


⚡️ 예시)
- 농구 선수 허훈의 자유투 성공 확률이 90%일 때, 3번째 실패가 나올 때 까지 성공시킨 자유투가 10번일 확률

2. 연속형 확률 분포
📍 확률밀도함수(probability density function)
- 연속형 확률 변수 X에 대해서 함수 f(x) 가 아래의 조건을 만족하면 확률밀도함수라고 한다.

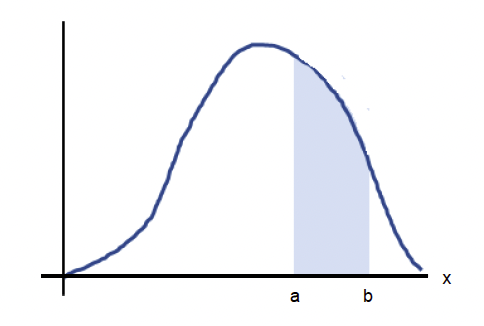
⚡️ 확률 밀도 함수의 성질

⚡️ 확률밀도함수의 평균과 분산
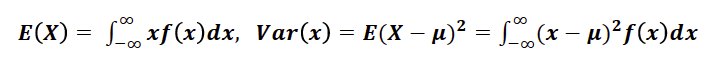
📍 누적분포함수(cumulative density function)
- 확률밀도함수를 적분하면 누적분포함수가 됨


⚡️ 누적분포함수의 성질

📍 균일분포(uniform distribution)
- 확률 변수가 X가 a와 b사이에서 아래와 같은 확률 밀도 함수(pdf)를 같음

⚡️ 균일 분포의 평균과 분산
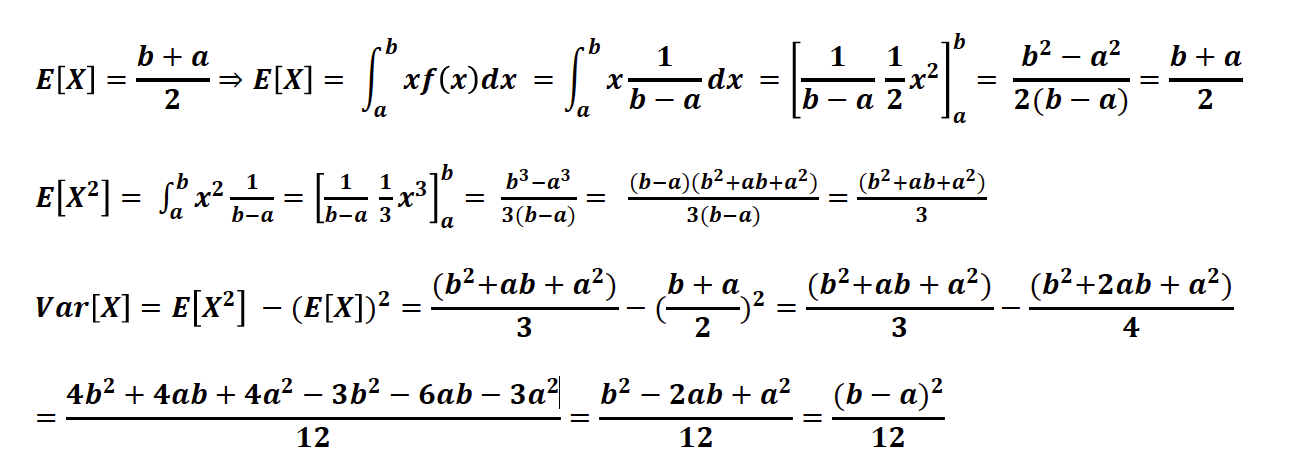
📍 정규 분포(normal distribution)
- 정규 분포는 19세기 최대 수학자라고 불리는 독일의 가우스에 의해 제시된 것으로 가우스 분포라고도 한다.

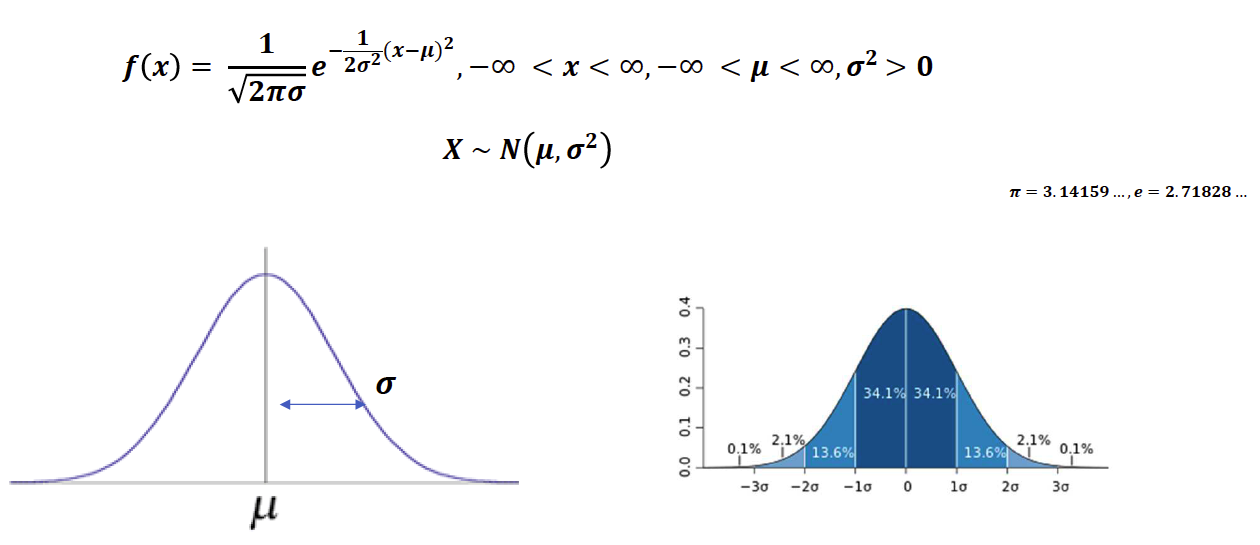
⚡️ 정규 분포(normal distribution)의 평균과 분산


⚡️ 파라미터의 따른 정규 분포 모양 비교
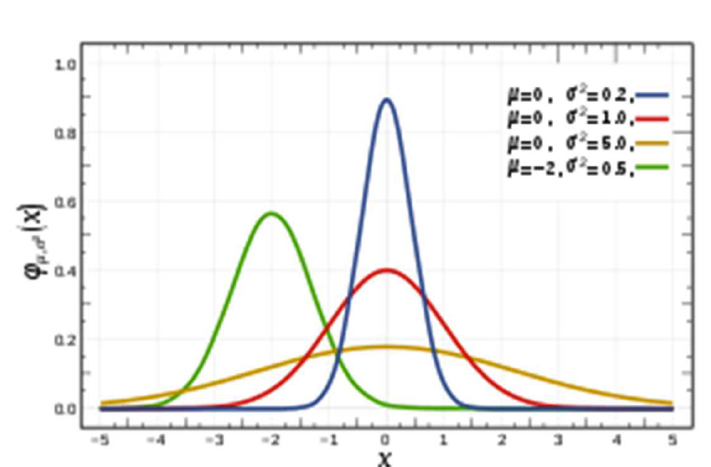
⚡️ 표준 정규 분포(standard normal distribution)


⚡️ 정규 분포의 성질

⚡️ 이항분포의 정규 근사
X ~ B(n, p) 일 때, 확률 변수 X는 n이 충분히 크면 근사적으로 정규 분포 X ~ N(np, np(1-p))를 따름


📍 지수분포(exponential distribution)

할때까지 걸린 시간 확률 변수 X는 지수 분포이다.
⚡️ 예시)
- 버스 정류장에서 100번 버스가 도착하는 횟수가 포아송 분포를 따른다면, 첫 번째 버스가 도착할 때까지 대기 시간의 분포가 지수분포이다.
⚡️ 지수 분포의 pdf


⚡️ 지수 분포의 cdf

- 지수 분포는 연속 되는 사건의 사이의 대기 시간도 지수 분포이다
- 즉 앞의 예시에서 두 번째 버스가 도착하고 세 번째 버스가 도착 할 때까지 대기 시간의 분포도 지수 분포이다.
⚡️ 지수 분포의 평균과 분산


⚡️ 지수분포의 무기억성 (Memoryless Property)

- 어떤 시점 부터 소요되는 시간은 과거 시간에 영향을 받지 않음
- 예시) 버스를 기다리는 대기시간은 먼저 기다린 사람과 확률이 같음
- 전구를 한달 동안 사용 했을 때 남은 수명은 한달 간 사용했던 영향을 받지 않음, 즉 새전구와 한달 간 사용한 전구의 남은 수명은 같다고 생각함
- 이런 문제로 실제 적용에 문제가 있고, 생존 분석에서는 Weibull 분포 또는 log-normal 분포를 사용하여 예측함
⚡️지수분포와 포아송 분포의 관계


반응형
'zero-base 데이터 취업 스쿨 > 스터디 노트' 카테고리의 다른 글
| [스터디 노트] Week12_1일차 [1 ~ 3] - ML (1) | 2023.10.10 |
|---|---|
| [스터디 노트] Week10_3일차 [기본] - 통계학 (1) | 2023.09.11 |
| [스터디 노트] Week10_1일차 [기본] - 통계학 (2) | 2023.09.11 |
| [스터디 노트] Week9_4일차 [심화_8 ~ 10] - SQL (0) | 2023.09.04 |
| [스터디 노트] Week9_3일차 [심화_5 ~ 7] - SQL (2) | 2023.09.04 |




